Đề Cương Ôn Tập HK2 Môn Toán Lớp 10 Trường Chuyên Bảo Lộc - Lâm Đồng Năm Học 2020 - 2021

Đề Cương Ôn Tập HK2 Môn Toán Lớp 10 Trường THPT Chuyên Bảo Lộc - Lâm Đồng Năm Học 2020 - 2021

MeToan.Com xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề cương ôn tập học kỳ 2 môn Toán 10 năm học 2020 - 2021 của trường THPT chuyên Bảo Lộc, tỉnh Lâm Đồng.

A. DÀNH CHO HỌC SINH LỚP TOÁN CƠ BẢN

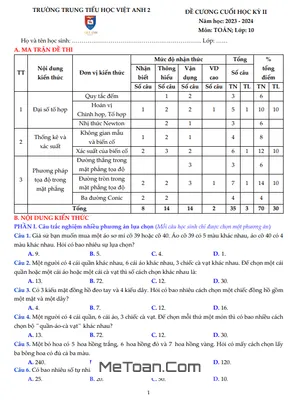
I. ĐẠI SỐ

1. Bất đẳng thức:
2. Xét dấu nhị thức, tam thức bậc hai: Giải phương trình, bất phương trình qui về bậc nhất; bậc hai; phương trình có chứa căn, trị tuyệt đối, tìm điều kiện phương trình, bất phương trình có nghiệm, vô nghiệm, có nghiệm thỏa mãn điều kiện.
3. Giải hệ bất phương trình bậc hai.
4. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn; ứng dụng vào bài toán tối ưu.
5. Tính tần số; tần suất các đặc trưng mẫu; vẽ biểu đồ biễu diễn tần số, tần suất (chủ yếu hình cột và đường gấp khúc).
6. Tính số trung bình, số trung vị, mốt, phương sai và độ lệch chuẩn của số liệu thống kê.
7. Tính giá trị lượng giác một cung, một biểu thức lượng giác.
8. Vận dụng các công thức lượng giác vào bài toán rút gọn hay chứng minh các đẳng thức lượng giác.

II. HÌNH HỌC

1. Hệ thức lượng trong tam giác.
2. Viết phương trình đường thẳng (tham số, tổng quát, chính tắc).
3. Xét vị trí tương đối điểm và đường thẳng; đường thẳng và đường thẳng.
4. Tính góc giữa hai đường thẳng; khoảng cách từ điểm đến đường thẳng.
5. Viết phương trình đường phân giác (trong và ngoài).
6. Viết phương trình đường tròn; xác định các yếu tố hình học của đường tròn. Viết phương trình tiếp tuyến của đường tròn; biết tiếp tuyến đi qua một điểm (trên hay ngoài đường tròn), song song, vuông góc một đường thẳng.
7. Viết phương trình chính tắc của elíp; xác định các yếu tố của elíp.

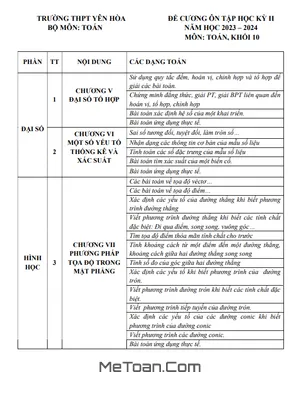
B. DÀNH CHO HỌC SINH LỚP CHUYÊN TOÁN

I. ĐẠI SỐ

• Bất đẳng thức và ứng dụng, bất phương trình, nhị thức bậc nhất, tam thức bậc hai và định lý đảo về dấu tam thức bậc hai, tỉ số lượng giác của một cung, một góc, công thức lượng giác.

II. HÌNH HỌC

• Hệ thức lượng trong đường tròn, phương trình đường thẳng, phương trình đường tròn, đường Elip.