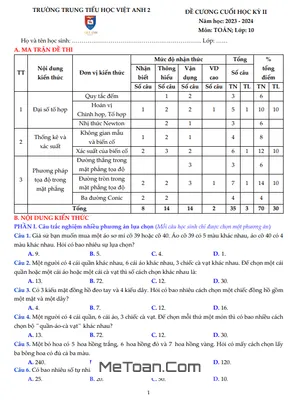
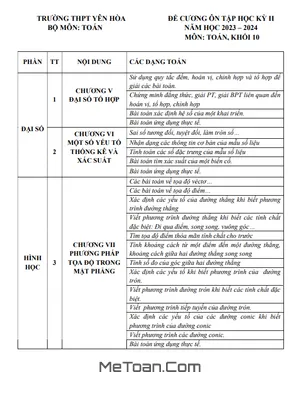
Đề Cương Ôn Tập Cuối Kì 2 Môn Toán Lớp 10 Năm 2024 - 2025 Trường THPT Nguyễn Việt Hồng – Cần Thơ

Đề Cương Ôn Tập Kiểm Tra Cuối Học Kì 2 Môn Toán 10 Năm 2024 - 2025
Trường THPT Nguyễn Việt Hồng – Cần Thơ
MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề cương ôn tập kiểm tra cuối học kì 2 môn Toán 10 năm học 2024 – 2025 trường THPT Nguyễn Việt Hồng, thành phố Cần Thơ.
Nội dung ôn tập:
1. Đại số:
1.1. Công thức tổ hợp và nhị thức Niu-Tơn.
- Công thức tổ hợp, chỉnh hợp, hoán vị.
- Nhị thức Niu-tơn, các bài toán liên quan.
1.2. Thu thập, tổ chức, phân tích và xử lí dữ liệu.
- Tính số đặc trưng đo xu thế trung tâm: số trung bình, trung vị, tứ phân vị, mốt.
- Giải thích ý nghĩa và vai trò của các số đặc trưng đo xu thế trung tâm.
- Tính số đặc trưng đo mức độ phân tán: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn.
- Giải thích ý nghĩa và vai trò của các số đặc trưng đo mức độ phân tán.
- Nhận biết mối liên hệ giữa thống kê với các môn học khác và trong thực tiễn.
- Phát hiện và lí giải số liệu không chính xác dựa trên mối liên hệ toán học đơn giản.
1.3. Khái niệm về xác suất – Các quy tắc tính xác suất.
- Mô tả không gian mẫu, biến cố trong thí nghiệm đơn giản (tung đồng xu, tung xúc xắc).
- Các khái niệm: phép thử ngẫu nhiên, không gian mẫu, biến cố, biến cố đối, định nghĩa cổ điển của xác suất, nguyên lí xác suất bé.
- Tính xác suất của biến cố bằng phương pháp tổ hợp (xác suất phân bố đều).
- Tính xác suất bằng sơ đồ hình cây (ví dụ: tung xúc xắc).
- Các tính chất cơ bản của xác suất.
2. Hình học:
1.4. Đường thẳng trong mặt phẳng Oxy.
- Viết phương trình đường thẳng.
- Tính khoảng cách từ một điểm đến đường thẳng.
- Tìm tọa độ giao điểm của hai đường thẳng.
1.5. Đường tròn trong mặt phẳng tọa độ và ứng dụng.
- Thiết lập phương trình đường tròn khi biết tâm và bán kính; biết tọa độ 3 điểm đường tròn đi qua.
- Xác định tâm và bán kính đường tròn khi biết phương trình.
- Thiết lập phương trình tiếp tuyến của đường tròn khi biết tọa độ tiếp điểm.
- Vận dụng kiến thức đường tròn để giải bài toán thực tiễn (ví dụ: chuyển động tròn trong Vật lí).
1.6. Ba đường Cônic trong mặt phẳng tọa độ và ứng dụng.
- Nhận biết ba đường conic bằng hình học.
- Nhận biết phương trình chính tắc của ba đường conic.
- Giải quyết vấn đề thực tiễn gắn với ba đường conic (ví dụ: hiện tượng trong Quang học).
- Đề cương có thể được điều chỉnh cho phù hợp với tình hình thực tế của nhà trường.
- Học sinh cần kết hợp học tập trên lớp, tự nghiên cứu và làm bài tập để đạt kết quả tốt trong kì thi.
Xem trước file PDF (393.7KB)
Share: